|
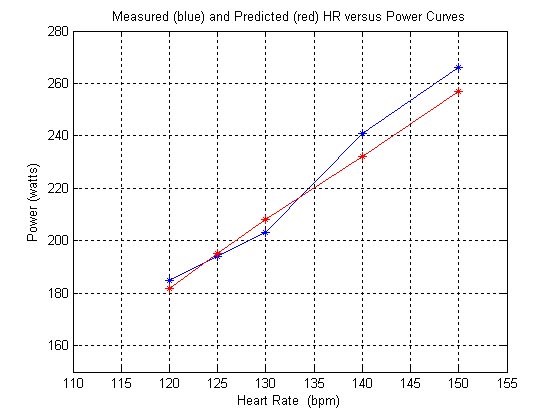
Using VO2max: Men: C/min = (-59.3954 + (-36.3781 + 0.271 x age + 0.394 x weight + 0.404 x VO2max + 0.634 x HR))/4.184 Women: C/min = (-59.3954 + (0.274 x age + 0.103 x weight + 0.380 x VO2max + 0.450 x HR)) / 4.184 Without VO2max: Men: C/min = (-55.0969 + 0.6309 x HR + 0.1988 x weight + 0.2017 x age) / 4.184 Women: C/min = (-20.4022 + 0.4472 x HR - 0.1263 x weight + 0.074 x age) / 4.184 where weight is in kilograms and C stands for Kcals. In order to assess the accuracy of the predictive equations, I have entered my individual physiological parameters (male, age = 53 , weight = 158) and plotted the predicted values (red line) against measured values (blue line) for my heart rate versus power. Using a bike trainer with a watt meter, I measured my power output for different heart rates, holding each data point for at least 10 minutes. For me, there was good agreement between the measured and predicted curves. This may not be the case for others. In fact , there was terrible agreement between the Kcals given by my Sigma Sport heart rate monitor and these equations. Note that the measured curve is approximately linear as predicted by the model equations. If I repeated these measurements I would find variation in my power output versus heart rate, depending on how I felt that day. One last item. If you believe the Calorie (Kcal) function of your heart rate monitor is accurate, you can convert Kcals/ hour to Watts and thus use it as a power meter. However, I would take any results with a grain of salt, as most heart rate monitors are not very accurate when it comes to estimating calories burned as a function of heart rate. You can increase the accuracy of estimating your power by holding your heart rate steady during the measuring process. Assuming 24% effieciency, Watts=(Kcals/hour)*1000/3600. I have provided a calculator script below which does the calculations for 2 different efficiency values. The efficiency of your body in transforming chemical energy to mechanical energy for cycling is anywhere between 20 to 25%, with most people falling in the middle of that range. Yes, that includes pros too. Yes, they produce gobs of power, but they require gobs of calories to do it. 24% is a commonly used efficiency because it makes the numbers come out nice. All that being said, if you run the numbers and find you are putting out more power than a member of the pro peleton, don't believe it. Assume the Kcal/hour output of your heart rate monitor is in error. :-) |